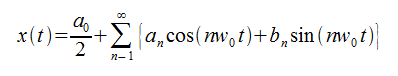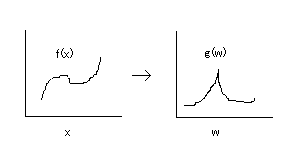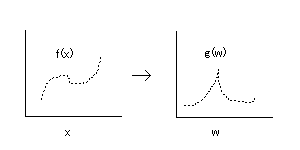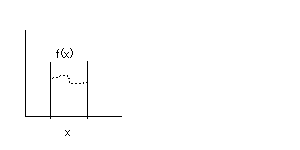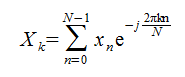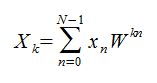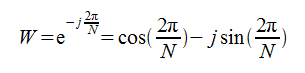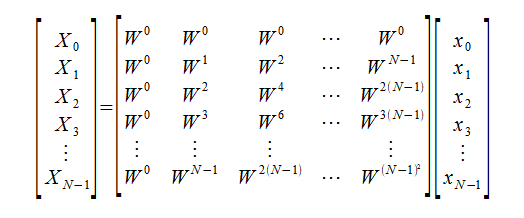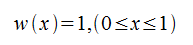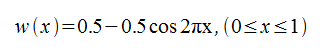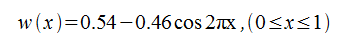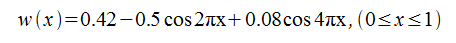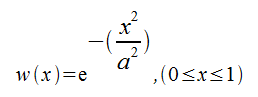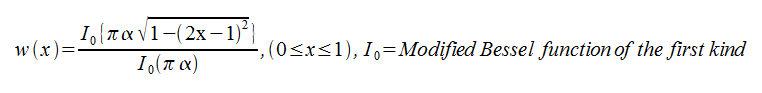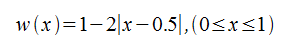FFTの基礎知識
■はじめに
dsPICの特徴にFFTの利用があります。dsPICの活用に先立ちFFTについての基礎知識をまとめます。
FFTの理解なしにはdsPICを活用することができないといっても過言ではありません。
FFTについてはさまざまな解説書があります。
数式やアルゴリズムの解説はされているものの、その「本質」を解説したものはいまだに見かけたことがありません。
私自身の経験でも学生時代に散々数式やアルゴリズムについて叩き込まれましたが、その本質を教わったことはありませんでした。
ところがふとしたことをきっかけに、なぞが解けはじめることになります。
まさに目からうろこが落ち、今まで深い霧の中を歩いていたことが、嘘のように急に霧が晴れ、筋道が見えてきたのです。
今までばらばらだったものが有機的に結びつき始め、その全体像が見えはじめたのです。
ここでは細かい数式の解説は行いません。それは参考書を見ればよいだけのことですから。
その背景にあるもの、つまりは本質に迫ります。
すべてを解説しきれるものではありませんが、FFTの理解の助けになれば幸いです。
■フーリエ変換とは
●フーリエとはフランスの数学者でフーリエ級数、フーリエ変換の功績が知られています。
工学のとりわけ波形処理の分野でフーリエ変換が使われます。
それはなぜでしょうか?まずはフーリエ変換を使う意味を考えてみましょう。
フーリエの考え出したフーリエ級数は不思議な性質を持っており、どのような波形でもフーリエ級数(三角関数の無限級数)で表現できてしまいます。
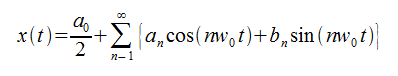
これは波形がさまざまな周波数の正弦波や余弦波の重ね合わせで成り立っていることを意味します(重ね合わせの原理)。
もし、波形をこのフーリエ級数に変換(フーリエ級数展開)できれば、周波数成分を知ることができます。
この変換をフーリエ変換と呼びます。逆に周波数成分から元の波形に変換することを逆フーリエ変換と呼びます。
矩形波を一度フーリエ変換し、さらに逆フーリエ変換して波形を戻す実験をしてみると面白いでしょう。
このようにフーリエ変換は波形の周波数成分(スペクトラム)を知ることができるため、
A/D変換とコンピュータの発達した現代において注目されています。
フーリエ変換の活用はこれだけに留まらず、いろいろな応用が考えられます。
150年以上後になって花咲くとはフーリエも予測できなかったことでしょう。
■FFTの背景
FFTとは高速フーリエ変換(Fast Fourier Transform)のことで、離散フーリエ変換(Discreate Fourier Transform)を
高速に計算するアルゴリズムです。ここまでがよく見る一般的な解説です。
ここにいくつかコンピュータ(計算学)と数学を結びつける重要なことが抜けて落ちています。
- フーリエ変換は積分の写像変換である。つまり「連続」している。
- フーリエ級数は理論上は無限である。つまり「有限」ではない。
- 工学とは技術を実用化する学問である。つまり「割り切り、妥協」が必要である。
一見、関連しそうもないことで、何のことやらわからないですが、これら3点はコンピュータと重要な結びつきがあります。
そもそもわれわれが知りたいのは「フーリエ変換の結果」です。なぜ離散フーリエ変換になり、なぜFFTなのでしょうか?
●連続では計算できない(線ではなく点でとらえる)
フーリエ変換は関数の写像変換です。写像変換とはある法則に則り、関数f(x)をg(w)に変換する作業のことです。
フーリエ変換の場合、変換法則が積分で表現されます。
関数f(x)も変数xも連続した値であり、フーリエ変換後の関数g(w)も変数wも連続した値です。
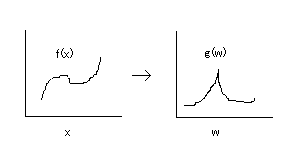
数学上はフーリエ変換を微積分を使って式を導くことができますが、
コンピュータ上では人間のように式を解くことはできません。
では仮にコンピュータでしらみつぶしに変数xを変化させて、f(x)を計算しようとしても、
変数xが「連続」であることから、永遠に計算しなければなりません(たとえば、1 と 2 の間には1.1 1.2 ...など永遠に細分化)。
これではどれだけ時間があっても計算が終わることはなく、フーリエ変換を解くことができません。
そこで「連続(線)」ではなく、ある飛び飛びの値(点)を使ってフーリエ変換の「大まかな」写像を捉えることにします。
たとえば、変数xに1,2,3...のような飛び飛びの整数を使います。これが離散と呼ばれる所以です。
連続した「線」ではなく、「点」の集まりで写像変換の全体像を捉えることにします。
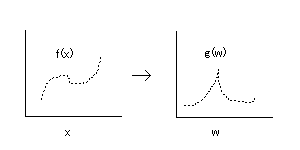
線から点に近似したため、誤差を生じます(離散化誤差)。
これがフーリエ変換をコンピュータ上で実現する第一歩になります。
A/D変換後のサンプリング・データを点として扱うことができる根拠になります。
●無限では計算できない(無限ではなく有限の区間を設ける)
かくして、コンピュータ上では「線」ではなく「点」の集まりでフーリエ変換を行うことになりますが、
実はこれだけではまだ計算できません。
「線」から「点」になることにより、フーリエ変換の法則は「無限積分」から「無限級数」に形を変えます。
積分は「線」にあたり、級数は「点」にあたりますが、「無限」の文字がまだ残ります。
つまり、級数を無限に計算しなければなりません。
これではどれだけ時間があっても計算が終わることはありません。
コンピュータは有限の時間で計算を打ち切る必要があります。
そこで変数の範囲を区切り、そこだけを計算することにします。この区間をフーリエ変換の世界では「窓」と呼びます。風景を窓で切り取るように、波形を切り取ります。
たとえば、変数xは0から100までの整数とします。
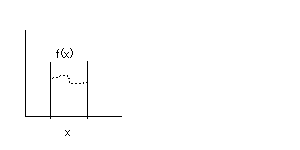
無限から有限に割り切り、妥協したことによって誤差を生じます。
とはいえ、「線」から「点」にさらに、区間を「無限」から「有限」に絞り込むことによって、やっとフーリエ変換を
計算できるようになります。これを離散フーリエ変換と呼びます。
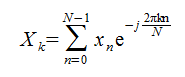
多少の犠牲(厳密性、精度など)を払っても計算できないよりできたほうが人間にとってメリットがあるのはいうまでもありません。
これがフーリエ変換をコンピュータ上で実現する第二歩になります。
A/D変換後のサンプリング・データを有限個に区切りって計算します。
●DFTは計算時間がかかり実用的ではない(計算方法を工夫したFFTの登場)
このように、本来は(連続)フーリエ変換の結果を知りたいのですが、それはコンピュータ上で
不可能であるため、妥協に妥協を重ねて、離散フーリエ変換(DFT)を計算します。
しかしDFTの計算は級数であり、大量の繰り返し演算を必要とします。
しかも精度を上げようとしてデータ数を増やすと、指数的(N2)に演算回数が増えます。
いくらコンピュータの進化した現代と言えども、計算時間を要します。
そこで演算回数を少なくする巧みなアルゴリズムが考えだされました。それがFFTです。
FFTは級数を行列演算として捉え、分割統治して演算します。行列の対象性に注目して演算回数を減らします。
FFTの演算回数はN・log2N /2 回になります。これをバタフライ演算とも呼びます。
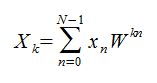
ただし
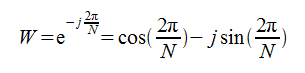
行列表現
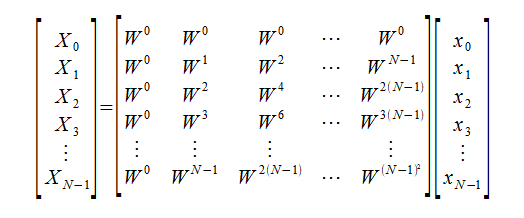
●工学と実用性(FFTは割り切りと妥協の産物)
フーリエ変換のために割り切って、妥協に妥協を重ねてきましたが、「実用性」が重要です。
これは工学に由来するものです。
悲しいかな工学は戦争とともに発展してきた事実もあります。弾道計算のためにコンピュータが開発されました。
工学では究極的に理論はどうあれ、技術をある程度実用化することに「意味と重点」を置いています。
ある程度の実用性があるなら、厳密な精度よりも実用性を重視します。
現在、気象予報にもスーパーコンピュータが活用されています。流体力学を基に天気予報を計算(多変量解析)しています。
精度の高い予報のためには、地球をより細かいメッシュ(格子)上に分割して計算する必要があります。
原理的には、空気の分子レベルまで細かくすれば、理論上正確な大気の動きを捉えることができます。
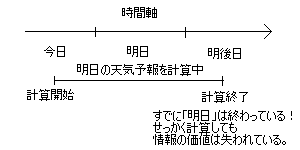
ただし、あまり細かくしてしまうと、演算回数が莫大になり、明日の天気予報の計算が明日中に
終わらなくなります。明後日(事後)になって明日の天気予報がわかったとしてもそれはすでに
「情報としての価値はなく」意味がありません。明日の天気予報が今日(事前)にわかるから情報の価値があります。
明日雨が降るとわかれば傘の準備をしますし、コンビニでは弁当の仕入れ数を減らすなどの調整をします。
つまり実用性が重要になります。
天気予報の演算もある程度の精度で割り切り、妥協して実用化されています。
フーリエ変換についても実用性が重要です。
たとえば新規開発したオーディオ機器の詳細な周波数特性を知るべくDFTを使って一年後に結果が得られたとしても
製品ライフサイクルの速い現代においてはもう販売終了しているでしょう。
つまり実用的な時間で解析する必要があります。
フーリエ変換をコンピュータ上で実現すべく、割り切りと妥協をしてきたDFTをさらに実用レベルに
するべく演算性能を工夫したFFTを利用しています。
このように FFT とはフーリエ変換をコンピュータ上で実現するための割り切りと妥協の産物といえます。
FFTの利用にあたっては、実用性を重視して、精度と計算速度のバランスをとる必要があります。
FFTを利用した時点で、厳密性は失われています。あくまでも近似結果です。この点を心に留めておきましょう。
■窓関数とは
FFTを利用する上で欠かすことのできない窓関数について解説します。
すでに解説したように、離散フーリエ変換をコンピュータ上で実現するためには、波形サンプルデータ数を有限に絞り込んでいます。
離散フーリエ変換ではこの波形データの一群が、永遠に繰り返されることを前提にしています。
(微分方程式の境界条件により、波形が無いことも、波形が繰り返されていることも同じ意味になります。)
つまり波形の初めと終わりがつながっていることを想定しています。
ところが実際には異なることが多く、不連続になってしまいます。
このままでは不連続な波形成分が抽出されてしまいます。
そこで、この不連続点の影響を少なくすべく、擬似的に不連続点を合わせるための関数を元の波形に掛け合わせます。
これを窓関数と呼びます。用途などに応じてさまざまな窓関数が考案されています。
いずれの窓関数も、波形の初めと終わりをつなげるように働き、波形の中心にはあまり影響を及ぼさないような関数です。
つまり不連続点の影響を最小限に抑えるため元の波形を加工することになります。
すでに解説したようにFFTを使用した時点で厳密性を失われており、窓関数の処理で不連続点の影響は取り除かれるもののさらに厳密性が損なわれます。
- 矩形窓(Rectangular window)
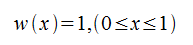
- ハニング窓(Hanning window)
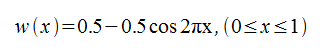
- ハミング窓(Hamming window)
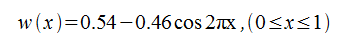
- ブラックマン窓(Blackman window)
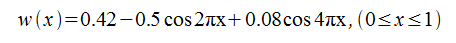
- ガウス窓(Gaussian window)
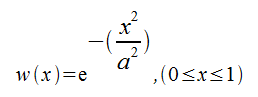
- カイザー窓(Kaiser window)
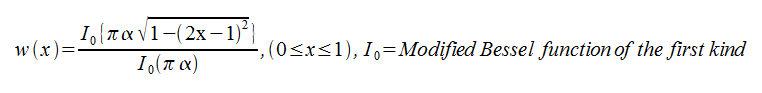
- バートレット窓(Bartlett window)
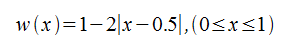
ハニング窓が一般的によく使われます。
■FFTを体感してみよう
さてFFTの理論や背景はこれくらいにして、実際に体験して見ましょう。
百聞は一見にしかず。
FFT.exe は Windows 上でFFTを体感するためのソフトウェアです。
波形の種類が限定されていたり、サンプリング数Nが固定であったりと制限がありますが、十分体感いただけるでしょう。
(1)FFT.exe をダウンロードし、起動します。
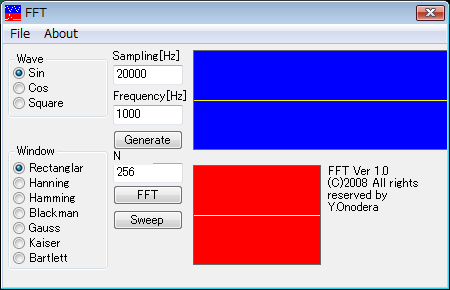
(2)波形の種類をWaveから選択し、サンプリング周波数(Sampling)と波形周波数(Frequency)の条件を指定して波形を生成(Generate)します。
A/D変換後のサンプリング・データが青色領域に表示されます(振幅は±1)。サンプリング定理を体感できます。
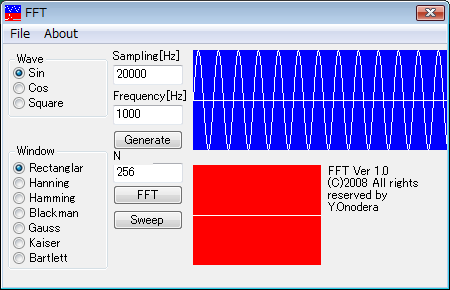
(3)窓関数を選択し、FFTを実行します。
青色領域に黄色で窓関数が表示されます。同時にFFT結果が赤色領域に表示されます。縦軸はdB(対数)表示です。これは窓関数の違いをわかりやすくするためと、実際に対数表示がよく使われるためです。
窓関数の違いを体験できます。
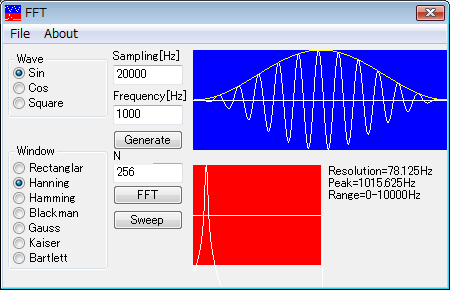
サンプリング数N=256ですので、横軸はその半分の128ポイントあります。
同時表示されるデータの意味は次のとおりです。
- Resolution= FFTの解像度(横軸)であり、1ポイントあたりの周波数間隔です。
- Peak= FFTのピーク周波数です。Resolutionの倍数になります。
- Range= FFTの横軸レンジ(周波数)です。
上記のハニング窓を使ったFFTでは、かなり鋭い周波数特性を示していますが、理論上のフーリエ変換では、
一つの周波数成分しか含まれていないので一つの縦線(もっと鋭い周波数特性)でなければなりません。
このようにFFTは近似結果となります。
●参考
- 高調波の重ね合わせでできている矩形波をFFTしてみると重ね合わせの意味がわかります。
- スイープ(Sweep)は周波数を整数で9倍まで自動的に波形の生成とFFTを行います。
- サンプリング数Nは固定です。表示上変更できますが、内部で固定されています。
- 一般的にハニング窓が使われる理由を理解できるでしょう。
- サンプリング定理に違反して、サンプリング周波数の半分以上の波形をFFTすると折り返しの周波数を確認できます。
- 矩形窓は窓関数なしと同じです。
- ガウス窓の係数aは1/sqr(2)です。
- カイザー窓の係数aは1です。
- 外部からサンプリング・データを入力できるようにすれば、その波形をFFTすることができます。
■ダウンロード
■履歴
| Version | date | 備考 |
| 1.0 | 2008-04-01 | リリース |
(C)2008 All rights reserved by Einstein.